Cavities: Photon Lifetime
The photon lifetime is a time constant that describes the decay (or the growth) of energy in a cavity. We can calculate the photon lifetime by considering the rate equation (a differential equation with time as the independent variable) for the decay of an initial bunch of photons, Np, in the cavity. The applet below shows a simple two mirror cavity with a "pulse" of photons bouncing back and forth.
Notice that the number of photons decays after each reflection from a mirror. The reflection of mirrors 1 and 2 in the picture are denoted as R1 and R2, respectively. The value of R will be from 1 to 0 (i.e., completely reflecting R = 1, and completely transmitting R = 0). The number of photons that left the cavity after one round trip is [1-S]Np, where S is called the survival factor and is R1*R2 for this two mirror cavity.
The photon lifetime for a cavity with refractive index n, and cavity length of l, is defined as:
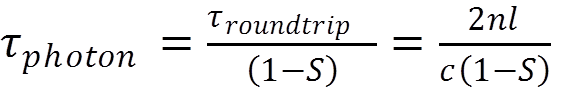
Comments
to anc@buffalo.edu
or vpc3@eng.buffalo.edu
Copyright (c) Prof. Alexander Cartwright and Vamsy Chodavarapu
Department of Electrical Engineering
University at Buffalo, 1999-2001